Grit Particle Settling – Refining The Approach

By Pat Herrick, Adam Neumayer, and Kwabena Osei - Hydro International

Summary

Grit settling velocity is significantly impacted by variability in size, density and shape. The conventional assumption of spheres with a specific gravity of 2.65 is inadequate for characterizing grit. Grit particles larger than 110 micron have a Reynolds number >1 therefore, Stokes’ Law is an oversimplification and should not be used in grit removal system design. Targeting 75-150 micron particle size for grit removal system design minimizes the impact of errors due to assumptions of ideal characteristics (e.g. spheres). Characterizing native grit physical particle size and settling velocity is the best means to determine grit removal system design requirements. In the absence of site specific characterization, regional grit gradation and settling velocity data should be used.

Introduction

Grit system design is heavily influenced by factors affecting the settling behavior of the targeted grit particle.¹ As such, the classic correlations of sedimentation for discrete solids, Stokes’ or Newton’s Law, are commonly used to guide design. To simplify the design process, it has been common to assume that grit is spherical with the density of silica sand. Unfortunately, grit particles are rarely ideal spheres with the assumed textbook density of 2.65 for silica sand. Less than ideal characteristics are frequently measured or observed.^1,2  By utilizing well established sedimentation theory corrections from other fields of engineering, these correlations can be refined to provide a useful tool to improve grit system design.

Grit particle settling is principally determined by size, density, homogeneity and shape with some industry accepted assumptions regarding the characteristics of the fluid. This can be seen in the particle settling velocity equation below as determined by Newton’s Law.³

V_p = g(ρ_p – ρ_w)d_p² / 18μ = g(sg_p – 1)d_p² / 18v

Size is most typically measured in terms of the mean diameter. In the last few years, density and shape implications are also being considered as a key aspect of grit behavior.²  It has been observed that particle density and shape do not align with traditional assumptions which necessitates the refinement of sedimentation calculations. Further, grit can be affected by attached materials such as fats, oils, and grease which impact the settling velocity.⁴  Below (see Figure 1) are pictures of individual clean  silica sand grains and similar sized grit particles (see Figure 2). It can be seen that the clean sand particles have a more rounded shape while the grit particles are more heterogeneous, angular shaped and appear to have other materials attached to them.

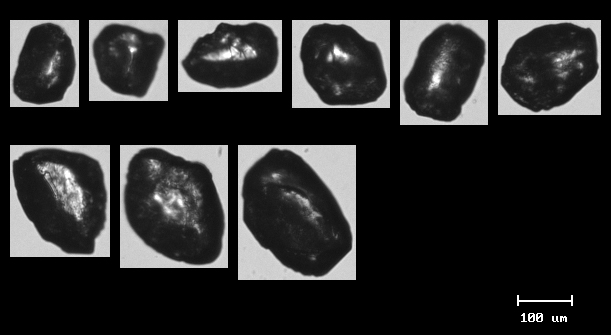
Figure 1. Clean silica sand as shown through digital imaging particle analysis
 

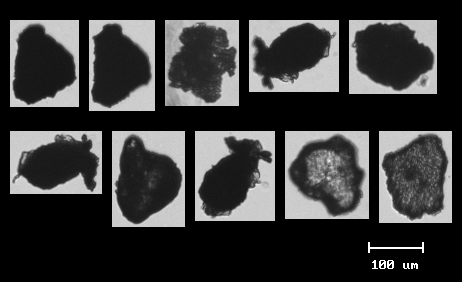
Figure 2. Wastewater grit as shown through digital imaging particle analysis.
Samples obtained at Muddy Creek WWTP, Cincinnati, OH

The net effect of the various deviations from "idealized” characteristics can be accounted for by measuring the true settling velocity of the grit particles. Figure 3 shows the nominal physical size versus the equivalent settling velocity of grit particles. This is often referred to as the Sand Equivalent Size (SES). SES is described as the equivalent sand particle having the same settling velocity as the slower settling endemic or native grit particle. The SES concept is discussed in more detail elsewhere.⁵ The diagonal black line in Figure 3 indicates the expected settling velocity based on conventional ideal assumptions. It can be seen that as the particle diameter gets larger than 100 micron, the settling velocity appears to be impacted more significantly by the deviations from the ideal characteristics. It is expected that this effect will diminish as the ratio of surface area to volume decreases with increasing particle diameters further to the right of the chart.

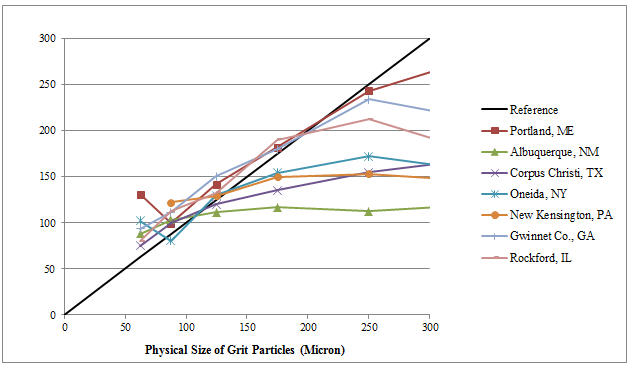
Figure 3. Physical size of grit particles vs. Sand Equivalent Size (SES) settling velocity

Stokes’ Law

Stokes’ Law is a common tool for estimating the settling velocity of grit particles, based on the assumption of laminar flow. It has been found to be accurate where Reynolds numbers are less than 1.²  A review of the Reynolds number for grit particles in the typical  design range of 50-500 micron for wastewater grit removal systems, shows that  the impact of transitional flow begins to affect particle settling above the 100 micron range resulting in a departure in predicted accuracy using Stokes’ Law. 

Table 1. Reynolds Number vs. diameter

Recommended Corrections

While a force balance requires an iterative process to determine settling velocity, it can be an irreplaceable tool by virtue of the physical characteristic corrections that can be layered in to refine the results towards real world measurements. Figure 4 illustrates the impact of eliminating common assumptions aimed at simplifying the calculation; and adding in refinements to align theory with field measurements. First, the settling velocity of a range of particle diameters is calculated using a laminar assumption (Stokes’ Law).2 Then the laminar assumption is removed resulting in a force balance (Newton’s Law).2 Subsequently, the assumption that grit / sand is a perfect sphere is eliminated and the equation is corrected for the angularity of the particles (Newton’s Law with Shape Factor).6,7,8 Then, an adjustment is made for the density of the particle based on field observations.9 Finally, all refinements are combined and plotted.  

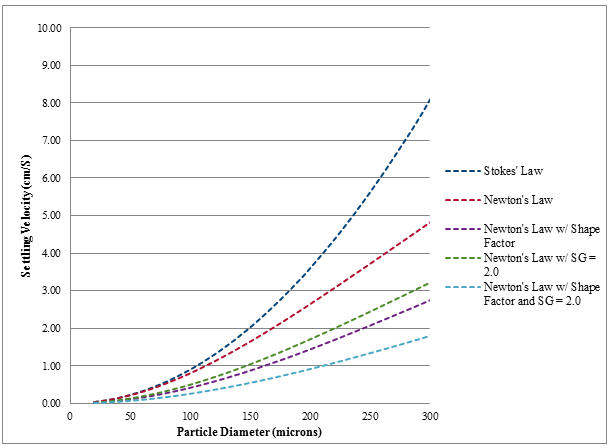
Figure 4. Settling velocity refinements – settling velocity vs. particle diameter

Overall, Figure 4 shows that the commonly used Stokes’ Law may not be the best approach to ensure an appropriate design to capture grit particles larger than 150 micron. Focusing on Newton’s Law, it can be seen that simply eliminating the laminar flow assumption in and of itself will result in a more conservative design in the critical 50-300 micron range. With each successive refinement, a level of realism is incorporated.

Table 2. Calculated particle settling velocity

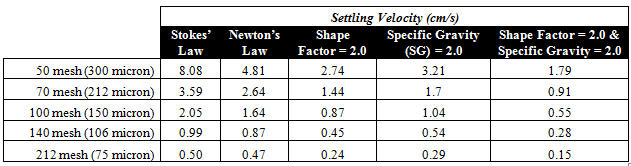
Figure 5 plots the physical size distribution of grit at a typical wastewater treatment plant as well as the sand equivalent size based on the settling velocity. It can be seen that nearly ~70% of the grit entering the plant is larger than 212 micron (75 mesh) based on physical size, yet only ~30% of the incoming grit settles as though it is larger than 212 micron. The 212 micron particle has a Reynolds number of 5.3 therefore Stokes’ is not an accurate equation for settling velocity of this and larger particle sizes. Based on Newton’s Law these 212 micron grit particles are expected to settle at a rate of 2.64 cm/sec. However, when adjusted for shape and SG, the calculated settling velocity is lowered to 0.91 cm/sec or roughly the equivalent of a 106 micron particle. Therefore, in order to remove 70 - 90% of the incoming grit load the system must be designed for 106 micron removal.

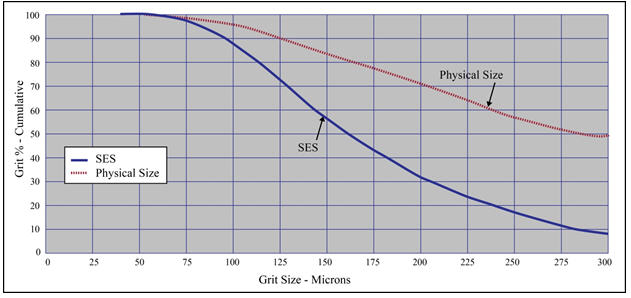
Figure 5. Measured physical size vs. settling velocity equivalent size (SES) at the East Regional WWTP Montgomery County, OH

In a very qualitative manner, we can layer measured settling velocity of grit particles on the calculated settling velocity chart to provide some sense of the validity of the refinements. This is shown in Figure 6.

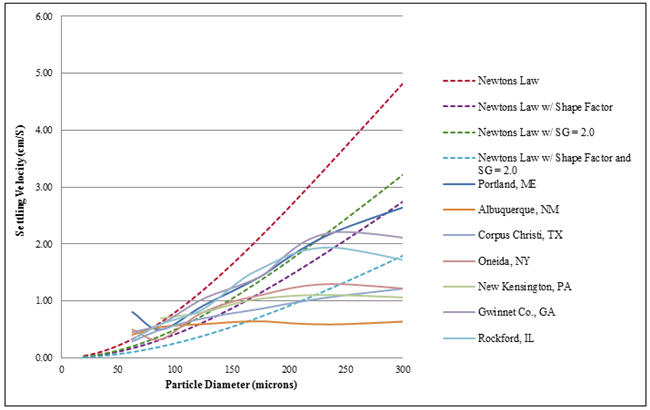
Figure 6. Measured settling velocity vs. calculated settling velocity

What can be taken from Figure 6 is that field measurements reinforce the idea that refinements to Newton’s law to account for shape and density narrow the gap between ideal theory and real world behavior. Accurately sizing a grit system can be a challenge given several variables that are often difficult to measure. Nevertheless, using widely available data on shape and density will certainly provide an increased level of reliability that a grit system will perform as anticipated.

Conclusions

• Grit settling velocity is significantly impacted by variability in size, density and shape. The conventional assumption of spheres with a specific gravity of 2.65 is inadequate.
• Grit particles larger than 110 micron have a Reynolds number >1 therefore, Stokes’ Law should not be used in grit removal system design for particles larger than 100 microns.
• Targeting 75-150 micron particle size for grit removal system design minimizes the impact of non-idealities.
• Characterizing native grit physical particle size and settling velocity is the best means to determine grit removal system design requirements.
• In the absence of site specific characterization, regional grit gradation and settling velocity data should be used for system design.

REFERENCES

1. Pretorius, C. (2012, October). A Review of Grit Basin Design. Presented at The Water Environment Federation Conference, New Orleans, LA, October 2012.
2. Boyrs, A.; Gabb, D.; & Hake, J. Performance Evaluation of Aerated Grit Chambers and Proposed Modifications to Increase Grit Removal Efficiency at East Bay Municipal Utility District WWTP. Presented at California Water Environment Association Annual Conference, Sacramento, CA, April 2002.
3. Tchobanoglous, G.; Burton, F. L.; Stensel, H. D.; & Metcalf & Eddy. Wastewater Engineering: Treatment and Reuse, 4th ed.; McGraw-Hill: Boston, 2003; pp 365.
4. Osei, K.; Gwinn, A.; Andoh, R.Y.G. Development of a Column to Measure Settling Velocity of Grit. Presented at World Environmental and Water Resources Congress, Albuquerque, NM, May 2012.
5. Kuchalwik, R. J. Critical Grit Removal Design Considerations for Retrofits and Additions at Existing Facilities. Presented at The Water Environment Federation Conference, New Orleans, LA, October 2012.
6. Letterman, R. D. (1999). Water Quality and Treatment, A Handbook of Community Water Supplies, AWWA, 5th ed.; Pearson.
7. Water Treatment Handbook, 7th ed.; Degrémont: Lavoisier: Paris, France, 2007.
8. Richardson, J.F.; Harker, J.H.; Backhurst, J.R. (2002). Coulson and Richardson's Chemical Engineering Volume 2 - Particle Technology and Separation Processes, 5th ed.; Elsevier, 2002.
9. Kivell, W. A.; Lund, N. B. Grit Removal: Some Fundamental Factors in Grit Separation and Grit Chamber Design. Water Works and Sewerage, 1941, pp 144.